Cosinusrelationerne:
a²=b²+c² - 2bc cos(A)
Ideen er at beregne kvadratet på den markerede højde 2 gange for at få opstillet en ligning. Denne ligning omformes til cosinusrelationerne. Her findes een af formlerne til beregning af siderne; de øvrige findes helt tilsvarende. For at beregne en vinkel løses ligningen blot for cos(A).
Bevis
Med Pythagoras sætning beregnes h 2 først i den røde retvinklede trekant, så i den blå:
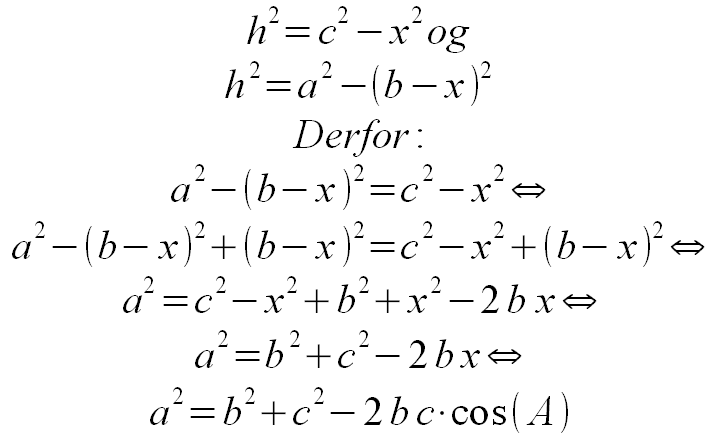
Hvis vinkel A er stump?
Træk punktet B over i venstre hjørne: Nu er A en stump vinkel. Bemærk ændringer i længdebetegnelser og kontroller, at de er rigtige. Igen beregnes kvadraterne på højden på næsten samme måde som før. I den røde trekant skal du bemærke, at den spidse (markerede) vinkel ved A ikke er A, men supplementvinklen: 180-A. Undervejs får du brug for formlen: cos(A) = - cos (180-A).
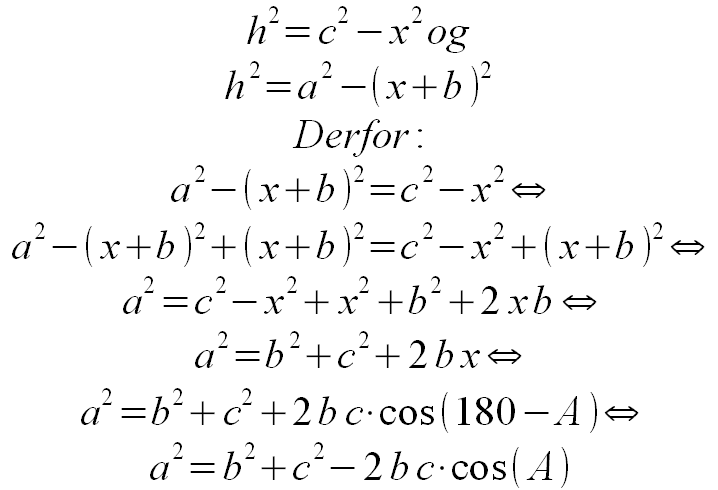
Hvis vinkel C er stump?
Træk punktet B over i højre hjørne: Nu er C en stump vinkel. Bemærk ændringer i længdebetegnelser og kontroller, at de er rigtige. Igen beregnes kvadraterne på højden på næsten samme måde som før. Og bemærk, at (b-x)² = (x-b)².
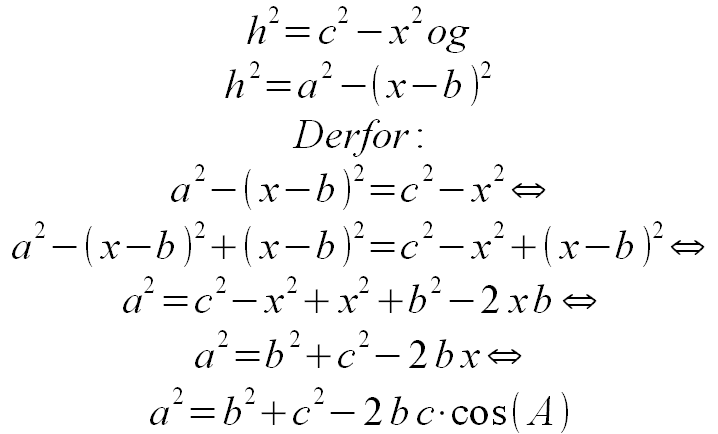
Ib Michelsen, Lavet med GeoGebra